The goal of entity matching in knowledge graphs is to identify sets of entities that refer to the same real-world object. Methods for entity matching in knowledge graphs, however, produce a collection of pairs of entities claimed to be duplicates. This collection that represents the sameAs relation may fail to satisfy some of its structural properties such as transitivity. We show that an ad-hoc enforcement of transitivity on the set of identified entity pairs may decrease precision. We therefore propose a methodology that starts with a given similarity measure, generates a set of entity pairs, and applies cluster editing to enforce transitivity, leading to overall improved performance.
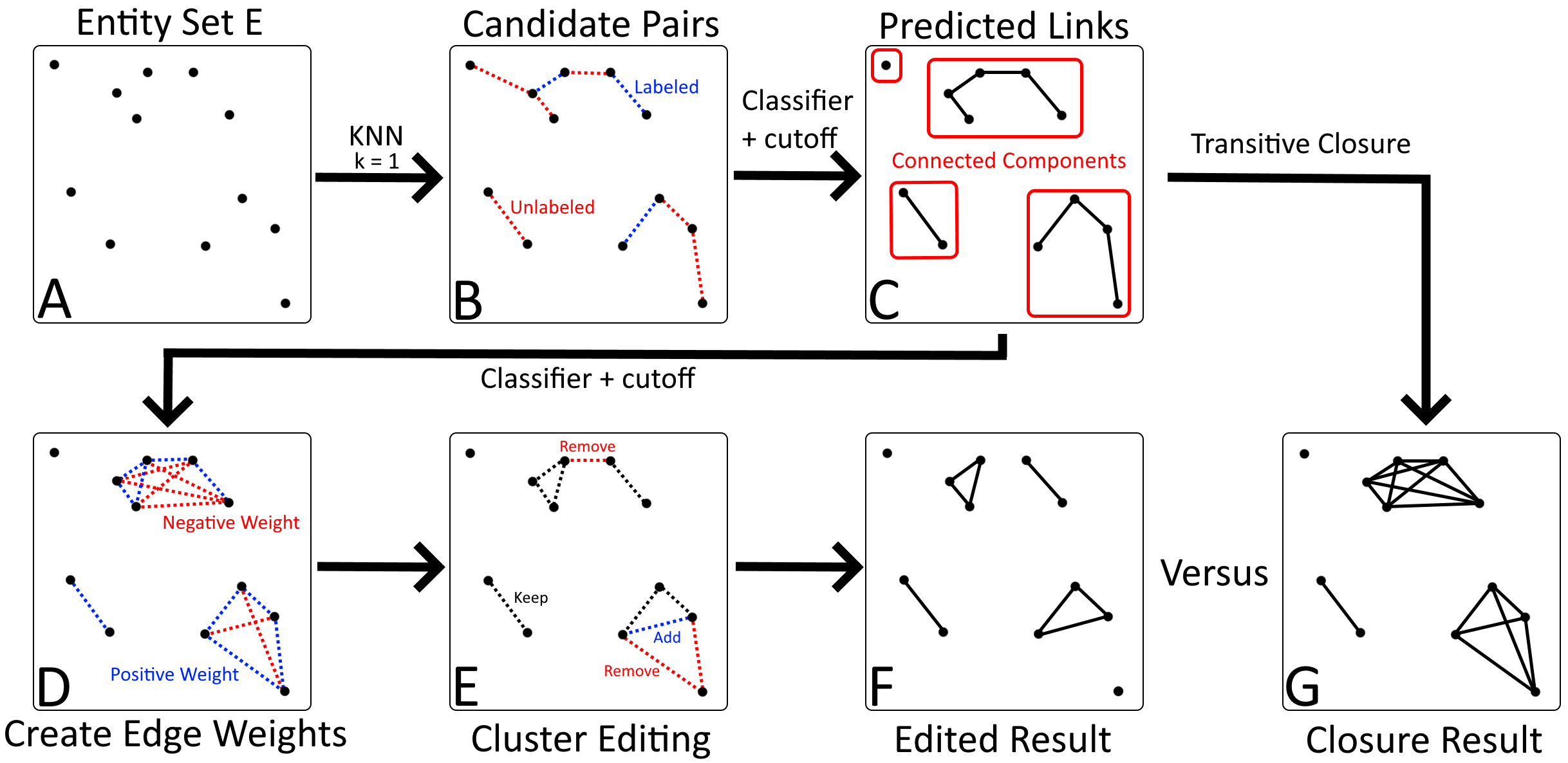
How transtivie closure and cluster edited results are calculated
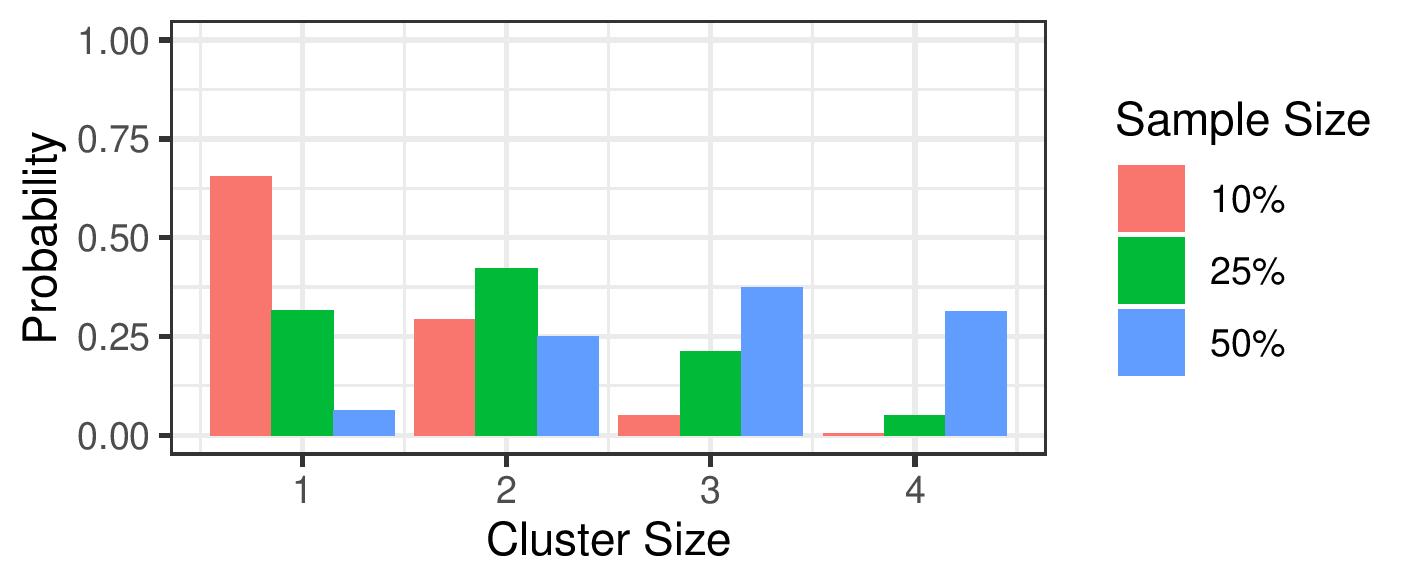
Generate random clusters with different sizes
The data source we use is an RDF version of Ecartico, a comprehensive collection of biographical data about, among others, painters, engravers and book sellers. These people worked in the Low Countries at the time of the 16th and 17th century. This data source is actively curated so we can be sure there are no duplicate records of persons. From the Ecartico graph, we have constructed a new graph containing all schema:Person entities that have values for the properties
- schema:name
- schema:workLocation
- schema:hasOccupation
For each of these entities, we also copy the property-values (if available) for
- schema:birthDate
- schema:deathDate
- schema:birthPlace
- schema:deathPlace
Then we introduce duplicates by uniformly sampling a percentage of entities and altering their respective URI’s. For example, when sampling entities, an entity with URI www.data.uu.nl/1234 will be modified to www.data.uu.nl/1234/3.
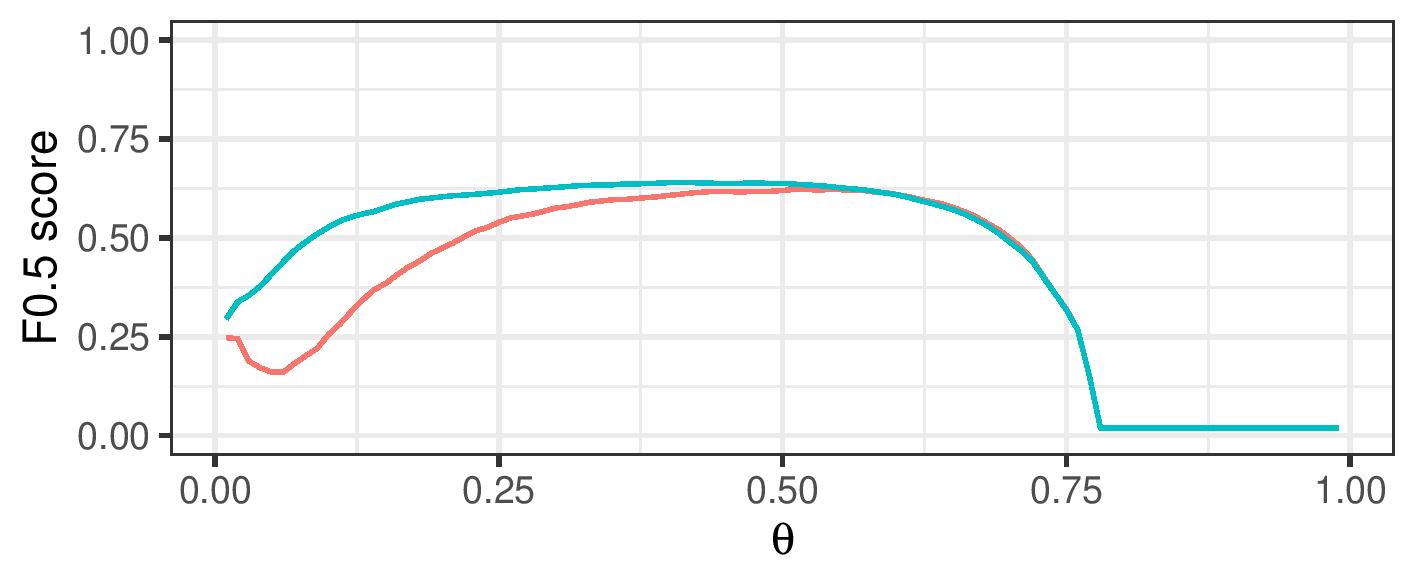
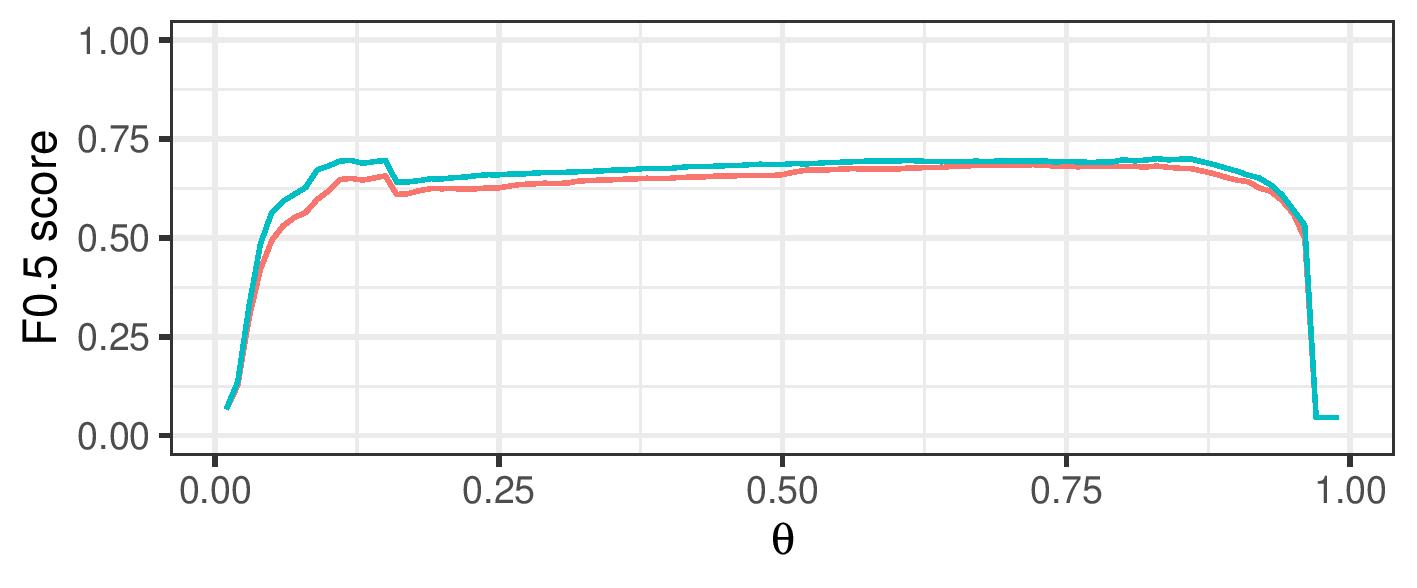
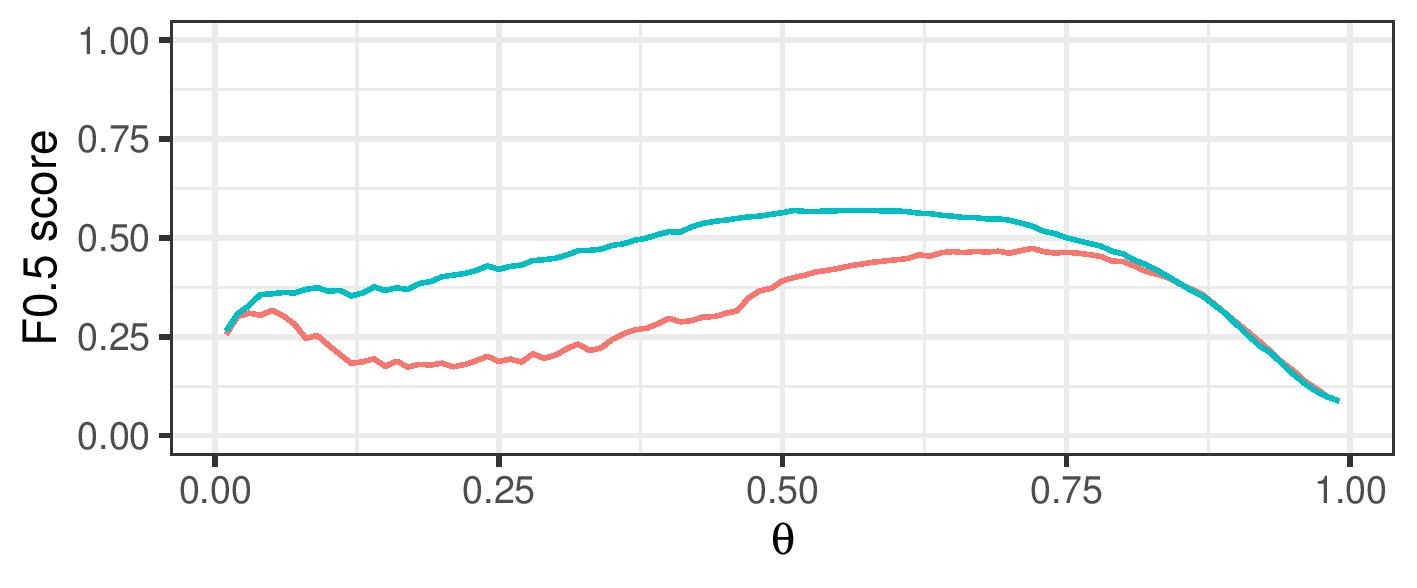
Improve F-0.5 score over a range of cutoff values
By using a range of cosine similarity cutoff values, we can generate connected components of different sizes. These components are then either treated as clusters themselves (transitive closure), or split up using cluster editing. The resulting (sub)clusters are then treated as referring to a single real-life entity.
| Feature: Cosine Similarity | Features: Hadamard Product |
|---|---|
 |
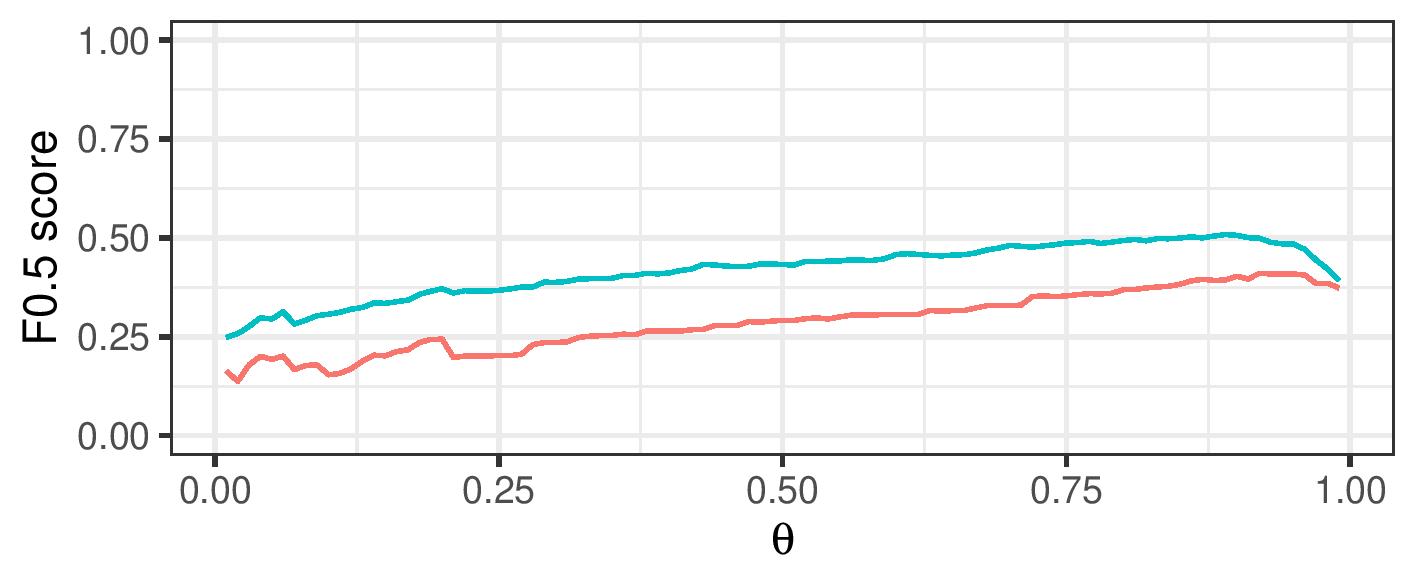 |
| Logistic Regression | Logistic Regression |
 |
 |
| SVM | SVM |